경사하강법
지금까지 배운걸 정리하면
사용자의 성적값이 주어지면
컴퓨터가 w 값을 구한다음
중간층에 분류를 해서 계산을 하고
계산된 값을 sigmoid 와같은 Activation fucntion 에 집어넣은 값을
최종 w 값과 계산해서 예측값을 도출해낸다고 했다.
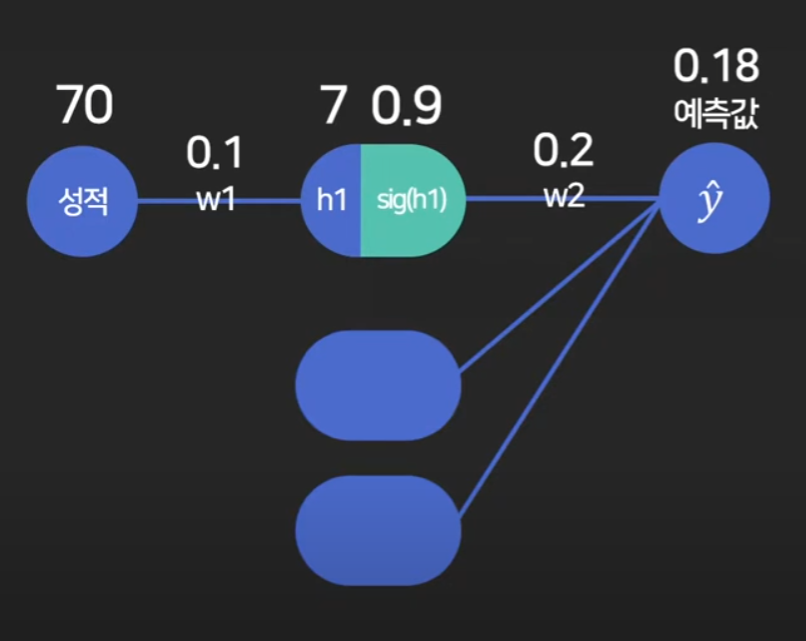
여기서 컴퓨터가 w를 구할때
실제 데이터와 비교한 후
loss를 구해서 loss를 최소화 하는 w를 찾아준다고 했는데
어떤 방식으로 찾는것일까??

쉬운 설명을 위해
w가 여러개있지만 w1만 예시로 들어보겠다
만약 임의로 w1에 0.5,0.7,0.2 이렇게 랜덤으로 데이터를 넣으면
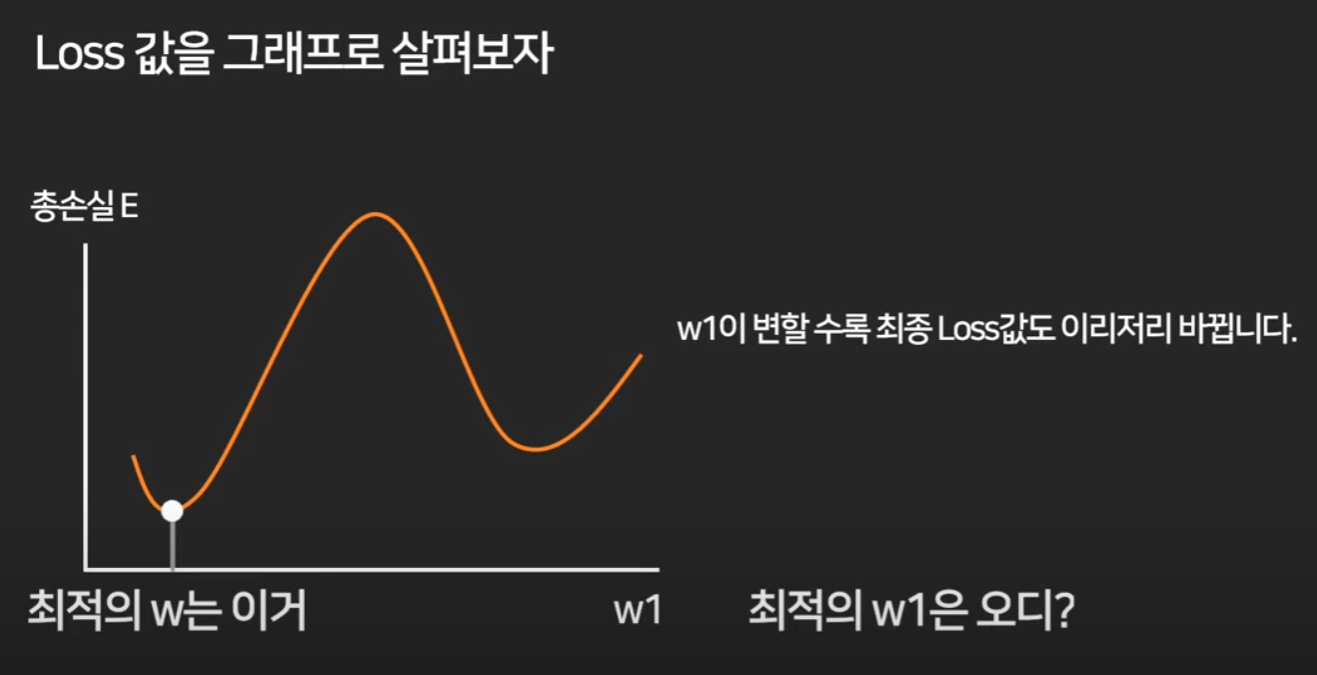
그에따라 총손실도 다 다른결과가 나올것인데

이를 그래프로 그리면 아래와 같을 것이다.

그렇다면 최적의 w1값은 어딜까
우리는 딱 보면 보인다. 하지만 컴퓨터는 어떻게 찾을까?
처음에는 랜덤값으로 아무대나 찍는다

예를들어 첫 값을 3으로 찍었다고 치자
그러면 이제 3이라는 위치에서 총손실값을 줄이는 방향으로 w값을 조정해야하는데
w값을 2로 옮기는게 좋을까 4로 옮기는게 좋을까?
당연 2로 옮기는게 좋다

하지만 지금은 변수하나만 예시로 들어서 2차원 그래프를 그려서 판단할 수 있었지만
실제 뉴럴네트워크는 w변수가 수십 수백개있어서
다차원 그래프는 우리가 그릴수도 없고 파악도 불가하다

그래서 사용하는 것이
경사하강법이다
현재 w 지점에서 기울기를 구한다음
w-기울기를 했을때
기울기가 양수면 왼쪽으로 이동할것이도
기울기가 음수이면 오른쪽으로 이동할 것이기때문에
최종적으로 기울기가 0인지점으로 이동할수 있게 된다

이걸 수식으로 표현하면 아래와 같다
w 원에서 w지점의 값을 미분한 값을 뺀것이다
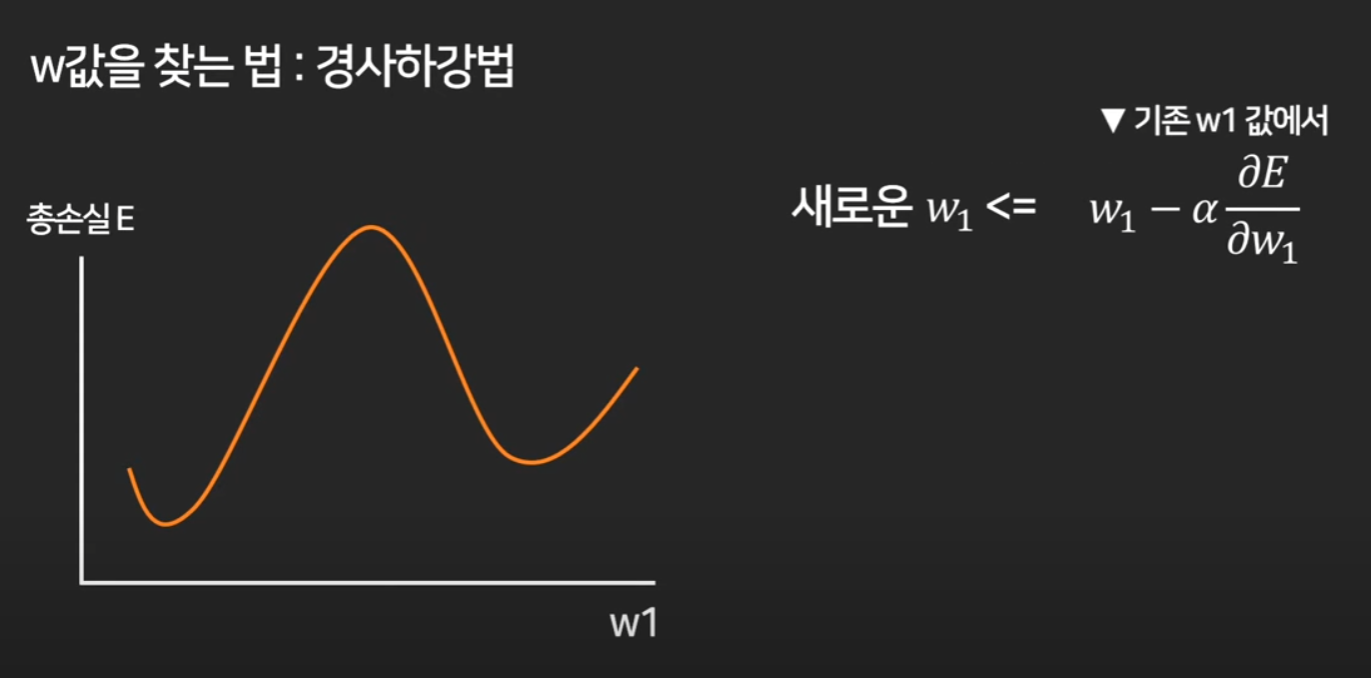
그래서
머신에게 러닝을 시킨다
= 손실을 최소하하는 w값 찾게 시킴
= 그방법은 경사하강
라고 보면된다.

그러면 w값이 갱신이 될것이다

새로운 딥러닝 뉴럴 네트워크가 나올것이다
거기서 이제 또 로스값을 계산하고 w값 수정하고 로스값 계산...

그래서 총손실이 더이상 안줄어들때까지 계산을 반복하는 것이다

이거를 파이썬 코드로 표현하면 아래와 같을 것이다.

근데 문제가 하나 있다
만약 더이상 줄어들지 않는 지점을 찾았는데 아래와 같은 결과라면?

더 최저점이 있는데 최저점이 아닌곳에서 학습을 끝내버리면 안된다.
그래서 이 현상을 방지하기 위한 방법이 하나있다
바로 learning rate 라는것을 곱해서 빼주는 것이다
그래서 저 미분한 값 앞에 알파값이 바로 learning rate 이다.

그러면 한번 이동할때 저 local minima라고 부르는 지역적인 부분에 있는 최저점을 넘어서
실제 최저점을 탐색할 수 있게 된다
그게 learning rate의 역할이다.
그래서 learning rate 을 적절히 잘 설정해주는것이 중요한데
이거는 답이 없다. 실험적으로 파악해야한다.
보통은 0.01 또는 0.0001 이런식으로 작은값부터 많이 시작을 한다.

그리고 이 learning rate을 고정된 값만 주면 학습이 제대로 안일어 날 수 있다

그래서 학습이 일어날때마다 가변적으로 learning rate을 수정해줘야하는데
이걸 가변적으로 최적화해주는 것이 바로
Learning rate optimizer이다
여기에는 여러가지가 있는데
대표적인 예로
- Momentum
: 만약 기울기 값이 너무 가팔라서 w값이 크게 뛰어넘었다. 그러면 이 많이 뛰어넘을걸 기억해뒀다가 다음 변화를 줄때 조금더 많이 뛰어 넘을수 있게 관성을 적용하는 것이다.

- AdaGrad: 자주 변하는 w값은 learning rate를 작게(섬세하게 표현할수있도록)
자주 안변하는 값은 local minima에 빠진것같으니 learning rate을 크게해서 local minima를 벗어날수있도록
- RMSProp : AdaGrad인데 제곱한것
- AdaDelta : AdaGrad인데 a 너무 작아져서 학습안되는거 방지해줌
- Adam : RMSProp + Momentum
정해진건 없고 실험적으로 파악해야함
보통은 Adam을 사용한다. 대부분의 상황에서 잘나옴
암튼 중요한거는
저 기울기는 w1만 예시로 들어서 기울기로 표현해서 계산한거지만
실제로는 수십 차원으로 표현해야하는데 그거는 인간의 인식을 넘어선다.
그래서 tensorflow를 사용하는 것이다.

'AI > 🤖 딥러닝' 카테고리의 다른 글
| 딥러닝 | 초간단 예측 AI 만들기 (0) | 2024.08.17 |
|---|---|
| 딥러닝 | 활성함수(Activation Function) (0) | 2024.08.11 |
| 딥러닝 | Neural Network 계산, Loss function (0) | 2024.08.11 |
| 딥러닝 | 뉴럴 네트워크 (0) | 2024.08.11 |
| 딥러닝 | 딥러닝이란? (0) | 2024.08.11 |
