해시 함수
해시함수는 어떻게 구현할까요? 이것을 알기 위해서는 해시 함수를 구현할 때 고려할 것들을 알아야 합니다. 사실 코딩 테스트에서 해시 함수를 직접 구현하라는 문제가 나오는 경우는 거의 없습니다. 그리고 자바에서는 해시셋 혹은 해시맵이라는 표준 API를 제공하는데 이 클래스는 해시와 거의 동일하게 동작하므로 해시를 쉽게 사용할 수 있습니다. 하지만 해시의 원리를 이해하고 해시맵을 사용하면 좀 더 효율적으로 해시맵을 사용할 수 있으므로 한 번쯤은 해시 개념을 공부하기를 추천합니다.
해시 함수를 구현할 때 고려할 내용
첫 번째, 해시 함수가 변환한 값은 인덱스로 활용해야 하므로 해시 테이블의 크기를 넘으면 안됩니다. 다음 그림으로 예를 들겠습니다. 현재 해시 함수의 결과는 해시 테이블의 크기가 N이므로 인덱스 0~N-1 사이의 값을 내야 합니다.

두 번재, 해시 함수가 변환한 값의 충돌은 최대한 적게 발생해야 합니다. 충돌의 의미는 서로 다른 두 키에 대해 해싱 함수를 적용한 결과가 동일한 것을 의미합니다. 다음과 같이 홍길동과 홍길서를 해시 함수에 넣었을 때 둘 다 결과값이 1이면 저장 위치가 같습니다. 즉, 충돌이 발생합니다.

충돌이 최대한 적어야 한다고 이야기한 이유는 충돌이 아예 발생하지 않는 해시 함수는 거의 없기 때문입니다
자주 사용하는 해시 함수 알아보기
그러면 이제 실제로 자주 사용하는 해시 함수를 알아보겠습니다.
나눗셈법
나눗셈법은 가장 떠올리기 쉬운 단순한 해시 함수입니다. 나눗셈법(division method) 은 키를 소수로 나눈 나머지를 활요합니다. 이처럼 나머지를 취하는 연산을 모듈러 연산이라고 하며 연산자는 %로 표시합니다. 예를 들어 7%2 = 1입니다. 앞으로 나머지를 취하는 연산은 모듈러 연산이라고 하겠습니다. 나눗셈법을 수식으로 작성하면 다음과 같습니다.
h(x) = x mod k
x는 키, k는 소수입니다. 아주 간단하죠, 키를 소수로 나눈 나머지를 인덱스로 사용하는 겁니다. 나눗셈법을 그림으로 나타내면 다음과 같습니다.

나눗셈법에 소수가 아닌 15를 사용하면 어떻게 될까?
그런데 왜 소수로 나눌까요? 소수를 사용하는 이유는 다른 수를 사용할 때보다 충돌이 적기 때문입니다. 예를 들어 소수가 아닌 15를 나눗셈법에 적용했다고 해봅시다. 나눗셈법에 적용했다는 의미는 위 식에서 k에 15를 적용한다는 의미입니다. 이때 x가 3의 배수인 경우를 한번 보겠습니다. 다음 그림을 보면 규칙적으로 게속 같은 해시값이 반복되는 것을 알 수 있습니다.
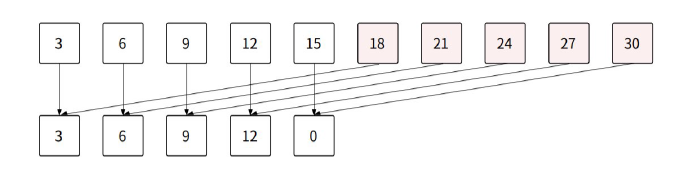
나눗셈법을 적용한 위 그림을 보면 x는 3의 배수, k는 15를 적용하면 수식은 h(x) = x mod 15(단, x는 3의 배수)가 됩니다. 이 식을 활용하면 해시값은 3, 6, 9, 12, 0 이 반복됩니다. 해시값을 보면 동일한 값들이 계속 반복되며, 이를 해시값이 충돌되었다고 표현합니다. 왜 그럴까요? x가 k의 약수 중 하나인 3의 배수이기 때문입니다. x를 5의 배수로 생각해도 충돌이 많이 발생합니다.
왜 충돌이 많이 발생할까?
이유는 생각보다 간단합니다. N의 약수 중 하나를 M이라고 한다면 임의의 수 K에 대해 M * K = N이 되는 수가 반드시 있습니다. 위 그림에서는 N이 15이고, M이 3인 경우입니다. 3 * 5 = 15이므로 K = 5 가 됩니다. 그리고 그림은 K를 주기로 같은 해시값이 반복됨을 알 수 있습니다. 따라서 K는 1과 자신 빼고는 약수가 없는 수, 즉, 소수를 사용하는 것이 좋습니다.
나눗셈법의 해시 테이블 크기는 K
그리고 나눗셈법은 해시 테이블의 크기가 자연스럽게 K가 됩니다. 왜냐하면 K에 대해 모듈러 연산을 했을 때 나올 수 있는 값은 0 ~ (K - 1)이기 때문입니다. 즉, 상황에 따라 아주 많은 데이터를 저장해야 한다면 굉장히 큰 소수가 필요할 수도 있습니다. 아쉽게도 매우 큰 소수를 구하는 효율적인 방법은 아직은 없으며 필요한 경우 기계적인 방법으로 구해야 합니다. 나눗셈법의 단점 중 하나입니다.
곱셈법
이번에는 곱셈법을 알아보겠습니다. 나눗셈법은 때에 따라 큰 소수를 사용해야 하는데 큰 소수를 구하기가 쉽지 않다는 단점이 있었습니다. 곱셈법은 나눗셈법과 비슷하게 모듈러 연산을 활용하지만 소수는 활요하지 않습니다. 곱셈법의 공식은 다음과 같습니다.
h(x) = (((x*A) mod 1) * m)
m은 최대 버킷의 개수, A는 황금비입니다. 황금비는무한소수로 대략 1.6180339887... 이며 이 책에서 계산에는 황금비의 소수부의 일부인 0.6183만 사용했습니다.
※ 황금비는 수학적으로 임의의 길이를 두 부분으로 나누었을 때, 전체와 긴 부분의 비율이 긴 부분과 짧은 부분의 비율과 같은 비율을 뜻합니다.
01단계
키에 황금비를 곱합니다

02단계
01단계에서 구한 값의 모듈러 1을 취합니다. 쉽게 말해 정수 부분을 버리고 소수 부분만 취합니다. 예를 들어 모듈러 1의 결과가 3.1523이면 0.1523만 취합니다. 소수 부분만 취하기 때문에 0.xxx 형태의 값이 나오게 됩니다.

03단계
02단계에서 구한 값을 가지고 실제 해시 테이블에 매핑합니다. 테이블의 크기가 m이면 02단계에서 구한 수에 m을 곱한 후 정수 부분을 취하는 연산을 통해 해시 테이블에 매핑할 수 있습니다. 02단계에서 구했던 값을 0.xxx의 값이므로 매핑할 테이블의 크기인 m을 곱하면 테이블의 인덱스인 0 ~ (m - 1)에 매치할 수 있습니다.

이처럼 곱셈법은 황금비를 사용하므로 나눗셈법처럼 소수가 필요 없다는 장점이 있습니다. 따라서 해시 테이블의 크기가 커져도 추가 작업이 필요 없습니다.
문자열 해싱
지금까지 알아본 해시 함수는 키의 자료형이 숫자였습니다. 이번에는 키의 자료형이 문자열일 때도 사용할 수 있는 해시 함수인 문자열 해싱을 알아보겠습니다. 문자열 해싱은 문자열의 문자를 숫자로 변환하고 이 숫자들을 다항식의 값으로 변환해서 해싱합니다. 공식은 다음과 같습니다.
※ 다음 함수는 문자열 해싱을 하기 위해 사용하는 polynomial rolling method입니다
hash(s) = (s[0] + s[1] * p +s[2] * p2 ... s[n-1] * pn-1 ) mod m
p는 31이고, m은 해시 테이블 최대 크기입니다. 이 수식이 실제 적용되는 과정을 그림과 함께 알아봅시다
※ p를 31로 정한 이유는 홀수이면서 메르센 소수이기 때문입니다.
※ 메르센 소수는 일반적으로 2N-1 형식으로 표시할 수 있는 숫자 중 소수인 수를 말합니다. 메르센 소수는 해시에서 충돌을 줄이는데 효과적이라는 연구 결과가 있습니다
01단계
다음 그림은 알파벳 a부터 z까지 숫자와 매치한 표와 키입니다.

02단계
"a"는 매치 표를 보면 1입니다. 따라서 "apple"의 "a"는 1입니다. 그러므로 수식의 s[0] * p0는 1 * 1이므로(31의 0승은 1입니다) 1입니다.

03단계
두 번째 문자열 "p"에 대해 연산을 진행합니다. "p"는 16입니다. 여기에 p1을 곱하면 496입니다.

04단계
이렇게 곱한 값들을 더하면 최종값은 4,990,970입니다. 이를 해시 테이블의 크기 m으로 모듈러 연산해 활용하면 됩니다.

기존에는 키 자체가 숫자였으므로 바로 해시 함수를 적용했지만 키가 문자열이면 각 문자열의 문자들을 적절한 숫자로 변경한 다음 해시 함수를 적용해야 합니다. 이런 변환 과정을 통해 문자열이 키인 데이터에도 해시를 사용할 수 있습니다. 하지만 해시 함수를 적용할 때 중요한 점이 있습니다. 해시 함수를 적용한 값이 해시 테이블 크기에 비해 너무 클 수 있다는 겁니다. 그래서 해시 함수가 내는 결과의 크기를 해시 테이블 크기에 맞도록 하는 작업이 필요합니다. 그림을 보면 "apple"이라는 간단한 문자열을 해싱했는데도 결과값은 4,990,970으로 굉장히 큽니다. 오버플로가 발생될 여지가 있으므로 다음 연산 버칩을 활요해 문자열 해시 함수를 수정할 수 있습니다.
문자열 해시 함수 수정하기
덧셈을 전부한 다음 모듈러 연산을 하는 왼쪽 수식 대신, 오른쪽 수식처럼 중간 중간 모듈러 연산을 해 더한 값을 모듈러 연산하면 오버플로를 최대한 방지할 수 있습니다.
(a + b)%c=(a%c+b%c)%c
이를 활용해서 앞서 본 문자열 해싱 공식을 수정하면 다음과 같습니다.
hash(s) = (s[0]%m+s[1]* p%m+s[2] * p2%m......s[n-1]*p(n-1)%m)%m
해시 함수뿐 아니라 보통 수식에 모듈러 연산이 있는 문제 중 큰수를 다루는 문제는 이런 오버플로 함정이 있는 경우가 많습니다. 난이도가 높은 문제는 대부분 이런 함정을 포함하고 있으니 이번 기회에 제대로 기억해두기 바랍니다.
'컴퓨터 과학 > 🔢 자료구조' 카테고리의 다른 글
| 트리 | 이진트리 (0) | 2024.11.24 |
|---|---|
| 트리 | 트리 개념 (1) | 2024.11.23 |
| 해시 | 충돌 처리 (0) | 2024.11.17 |
| 해시 (0) | 2024.11.17 |
| 큐 (11) | 2024.11.14 |
